자유로운 아이디어를 공유하는 곳!
글 수 561
큰구름의 수수께끼를 해 본 사람이라면 주름살이 뭔지 알 것이다.
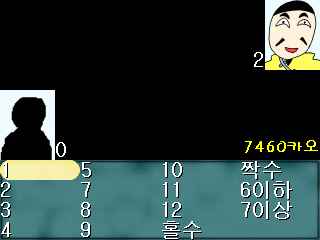
바로 이 게임.
내가 만들었기에도 뭐하지만 똑같은 카드 2세트를 들고 높은 숫자를 낸 사람이 이기는 단순한 게임이다.
완승을 가능하게 하기 위해서 큰구름의 수수께끼에서는 홀수, 짝수, 6이하, 7이상 카드가 존재한다.
이것도 나쁘지 않았지만 게임이 너무 길어지다 보니 긴장감이 없고,
카드가 너무 많으니 상대에게 남은 카드 기억하기도 어려워서 생각한 것이
카드를 5장으로 줄여서 가볍게 승부한다는 것이었다.
그것이 주름살5.
그리고 여기에는 1~5카드밖에 존재하지 않는다.
룰은 간단하게 높은 숫자를 낸 사람의 승리!
즉, 완승은 절대 할 수 없다. 최대가 4승 1패.
여기까지는 좋은데, 전 주름살에서 이긴 횟수에 따라 돈을 배로 가져간다는 도박성이 희박해진 듯하다.
전 주름살에서는 완승으로 32배까지 돈을 가져갈 수 있었다.
그래서 좀 더 도박성을 높이기 위해서
가져간 카드 수가 아닌, 가져간 카드의 숫자의 합계로 배율을 따지는 것이다.
이 경우 최고의 승리의 거두었을 때,
상대는 5와 1의 카드만 가져서 6점.
나는 나머지 카드를 모두 가져서 24점.
즉, 24 - 6 = 18배를 가져 갈 수 있게 된다.
배율은 이전의 32배에서 반 정도로 줄었지만,
카드가 5장이라서 승부 속도가 빠르므로 크게 문제 없다고 본다.
일단 여기까지 룰이 정리되자,
승부는 대충 어떻게 되는지 통계를 내어보고 싶었다.
일단 5장의 카드를 내는 순서는 5!으므로 120개의 순서가 존재.
상대도 역시 120개의 순서로 카드를 낼 수 있다.
즉, 승부의 형태는 120x120 = 14400의 경우가 생기게 된다.
난 수학을 못 하기 때문에 계산 같은 것을 못한다.
그러므로 프로그래밍으로 모든 상황을 시뮬레이트 해봤다.
그리고 아래는 그 중에 통계만 뽑아낸 것.
(14400번의 승부의 데이터는 wrinkle.zip의 result.txt를 보면 됩니다.)
통계
=================
승점 : 0, 발생빈도 : 4320(30.00%)
승점 : -8, 발생빈도 : 960(6.67%)
승점 : 8, 발생빈도 : 960(6.67%)
승점 : -6, 발생빈도 : 1560(10.83%)
승점 : -14, 발생빈도 : 240(1.67%)
승점 : 2, 발생빈도 : 600(4.17%)
승점 : 6, 발생빈도 : 1560(10.83%)
승점 : -2, 발생빈도 : 600(4.17%)
승점 : 14, 발생빈도 : 240(1.67%)
승점 : -4, 발생빈도 : 1080(7.50%)
승점 : -10, 발생빈도 : 360(2.50%)
승점 : -18, 발생빈도 : 120(0.83%)
승점 : -12, 발생빈도 : 120(0.83%)
승점 : 10, 발생빈도 : 360(2.50%)
승점 : 4, 발생빈도 : 1080(7.50%)
승점 : 18, 발생빈도 : 120(0.83%)
승점 : 12, 발생빈도 : 120(0.83%)
30% 확률로 무승부.
즉, 내가 이길 확률은 35%,
상대가 이길 확률은 35%가 된다.
1/3, 1/3, 1/3이 아닌게 조금 의외이지만 그 이유는 나중에 생각해 보기로 하고,
최고 승점인 18은 0.83%로 발생.
그리고 가장 흔한 승점은 2점이 아닌 6점.
이 점도 역시 확률의 재밌는 점이다.
이런 거에 관해서라면 이야기 파라독스를 보면 알 수 있겠지만, 접어두고.
아무튼 상당히 재밌게 즐길 수 있는 게임이 될 듯.
큰 구름의 수수께끼 후속작이 나오면 적용해봐야 겠다.
주름살5 승부 통계 소스

바로 이 게임.
내가 만들었기에도 뭐하지만 똑같은 카드 2세트를 들고 높은 숫자를 낸 사람이 이기는 단순한 게임이다.
완승을 가능하게 하기 위해서 큰구름의 수수께끼에서는 홀수, 짝수, 6이하, 7이상 카드가 존재한다.
이것도 나쁘지 않았지만 게임이 너무 길어지다 보니 긴장감이 없고,
카드가 너무 많으니 상대에게 남은 카드 기억하기도 어려워서 생각한 것이
카드를 5장으로 줄여서 가볍게 승부한다는 것이었다.
그것이 주름살5.
그리고 여기에는 1~5카드밖에 존재하지 않는다.
룰은 간단하게 높은 숫자를 낸 사람의 승리!
즉, 완승은 절대 할 수 없다. 최대가 4승 1패.
여기까지는 좋은데, 전 주름살에서 이긴 횟수에 따라 돈을 배로 가져간다는 도박성이 희박해진 듯하다.
전 주름살에서는 완승으로 32배까지 돈을 가져갈 수 있었다.
그래서 좀 더 도박성을 높이기 위해서
가져간 카드 수가 아닌, 가져간 카드의 숫자의 합계로 배율을 따지는 것이다.
이 경우 최고의 승리의 거두었을 때,
상대는 5와 1의 카드만 가져서 6점.
나는 나머지 카드를 모두 가져서 24점.
즉, 24 - 6 = 18배를 가져 갈 수 있게 된다.
배율은 이전의 32배에서 반 정도로 줄었지만,
카드가 5장이라서 승부 속도가 빠르므로 크게 문제 없다고 본다.
일단 여기까지 룰이 정리되자,
승부는 대충 어떻게 되는지 통계를 내어보고 싶었다.
일단 5장의 카드를 내는 순서는 5!으므로 120개의 순서가 존재.
상대도 역시 120개의 순서로 카드를 낼 수 있다.
즉, 승부의 형태는 120x120 = 14400의 경우가 생기게 된다.
난 수학을 못 하기 때문에 계산 같은 것을 못한다.
그러므로 프로그래밍으로 모든 상황을 시뮬레이트 해봤다.
그리고 아래는 그 중에 통계만 뽑아낸 것.
(14400번의 승부의 데이터는 wrinkle.zip의 result.txt를 보면 됩니다.)
통계
=================
승점 : 0, 발생빈도 : 4320(30.00%)
승점 : -8, 발생빈도 : 960(6.67%)
승점 : 8, 발생빈도 : 960(6.67%)
승점 : -6, 발생빈도 : 1560(10.83%)
승점 : -14, 발생빈도 : 240(1.67%)
승점 : 2, 발생빈도 : 600(4.17%)
승점 : 6, 발생빈도 : 1560(10.83%)
승점 : -2, 발생빈도 : 600(4.17%)
승점 : 14, 발생빈도 : 240(1.67%)
승점 : -4, 발생빈도 : 1080(7.50%)
승점 : -10, 발생빈도 : 360(2.50%)
승점 : -18, 발생빈도 : 120(0.83%)
승점 : -12, 발생빈도 : 120(0.83%)
승점 : 10, 발생빈도 : 360(2.50%)
승점 : 4, 발생빈도 : 1080(7.50%)
승점 : 18, 발생빈도 : 120(0.83%)
승점 : 12, 발생빈도 : 120(0.83%)
30% 확률로 무승부.
즉, 내가 이길 확률은 35%,
상대가 이길 확률은 35%가 된다.
1/3, 1/3, 1/3이 아닌게 조금 의외이지만 그 이유는 나중에 생각해 보기로 하고,
최고 승점인 18은 0.83%로 발생.
그리고 가장 흔한 승점은 2점이 아닌 6점.
이 점도 역시 확률의 재밌는 점이다.
이런 거에 관해서라면 이야기 파라독스를 보면 알 수 있겠지만, 접어두고.
아무튼 상당히 재밌게 즐길 수 있는 게임이 될 듯.
큰 구름의 수수께끼 후속작이 나오면 적용해봐야 겠다.
주름살5 승부 통계 소스